반응형
자료구조 분류
선형 자료구조 (Linear Data Structure): 데이터가 연속적 또는 순차적으로 저장
종류 : 배열 (Array) , 연결리스트(LinkedList), 스택(Stack), 큐(Queue)
비선형 자료구조 (Non-linear Data Strucure) : 데이터가 계층적 또는 네트워크 구조로 저장
종류 : 트리(Tree), 그래프(Graph)
선형 자료구조(Linear Daa Structure)
배열(Array)
정의
- 크기가 고저왼 연속정인 메모리 공간에 데이터를 저장
- 인덱스를 통해 데이터에 직접 접근
특징
- 연속된 메모리 공간 : 데이터의 물리적 순서와 논리적 순서가 동일
- 빠른 데이터 접근 : O(1)
- 고정 크기: 배열 서언 시 크기 결정
시간 복잡도
| 연산 | 시간 복잡도 |
| 접근 | O(1) |
| 탐색 | O(n) |
| 삽입/삭제 | O(n) |
활용 사례
고정크기 데이터 저장 (예 : 월별 매출 데이터)
요소가 자주 삭제되거나 추가 되지 않는다 ( 예 : 학생들 성적)
행렬 연산 (2D 배열)
연결리스트 (LinkedList)
정의
- 데이터가 노드(Node)에 저장디며, 각 노드는 다음 노드의 주소를 포함
- 메모리의 비연속적인 위치에 저장
구조
- 노드 : 데이터와 포인터로 구성
- 포인터 : 다음 노드의 주소를 저장료구조 분류
- 선형 자료구조 (Linear Data Structure): 데이터가 연속적 또는 순차적으로 저장
종류
- 단일 연결 리스트 (Singly Linked List) : 한 방향으로 연결

- 이중 연결 리스트(Doubly Linked List) : 앞뒤로 연결

- 원형 연결 리스트 (Circular Linked Lis) : 마지막 노드가 첫 노드를 본다
시간 복잡도:
연산 시간 복잡도
| 연산 | 시간 복잡도 |
| 접근 | O(n) |
| 탐색 | O(n) |
| 삽입/삭제 | O(1) |
활용 사례:
- 동적 데이터 관리.
- 대기열, 메모리 재활용.
- 작업 목록 관리 시스템에서 연결 리스트를 사용하여 작업을 추가하거나 삭제
스택 (Statck)
정의
- LIFO (Last In, First Out) 방식으로 동작하는 자료구조
- 마지막에 삽이뵌 데이터가 가장 먼저 삭제 된다.

구조
- Push : 데이터를 스택에 삽입
- Pop : 데이터를 스택에서 제거
- Top : 스택의 가장 상단 데이터를 확인
시간 복잡도
| 연산 | 시간 복잡도 |
| 삽입 | O(1) |
| 삭제 | O(1) |
| 접근 | O(1) |
활용 사례
- 함수 호출 스택
- 괄호 짝 검사
- 문자열 역순 출력
- 웹 브라우저의 뒤로 가기 기능은 스택을 활용하여 이전 페이지의 주소를 저장하고 차례대로 접근하는 방식
큐 (Queue)
정의
- FIFO (First In, First Out) 방식으로 동작하는 자료구조
- 먼저 삽이뵌 데이터가 먼저 삭제된다.

구조
- Enqueue : 데이터를 큐에 삽입
- Dequeue : 데이터를 큐에서 삭제
종류
- 원형 큐 (Circular Queue) : 큐의 공간을 재활용

- 우선순위 큐 ( Priority Queue) : 우선순위에 따라 데이터 처리

- 덱(Deque) 양쪽에서 삽입/ 삭제 가능

시간 복잡도
| 연산 | 시간 복잡도 |
| 삽입 | O(1) |
| 삭제 | O(1) |
활용 사례
- 작업 대기열
- 네트워크 패킷 처리
비선형 자료구조
트리(Tree)
정의
- 계층적 데이터 구조로 노드 간 부모-자식 관계를 표현
- 최상위 노드는 루트(Root), 자식 노드가 없는 노드는 리프(Leaf)

구조
- 루트 노드 : 트리의 최상위 노드
- 자식 노드 : 하위에 연결된 노드
- 서브트리 : 특징 노드와 그 하위 노드 집합
종류
- 이진 트리 (Binary Tree) : 각 노드가 최대 두 개의 자식을 가진다.

- 이진 탐색 트리 (Binary Search Tress, BST) : 왼쪽 자식 < 부모 < 오른쪽 자식
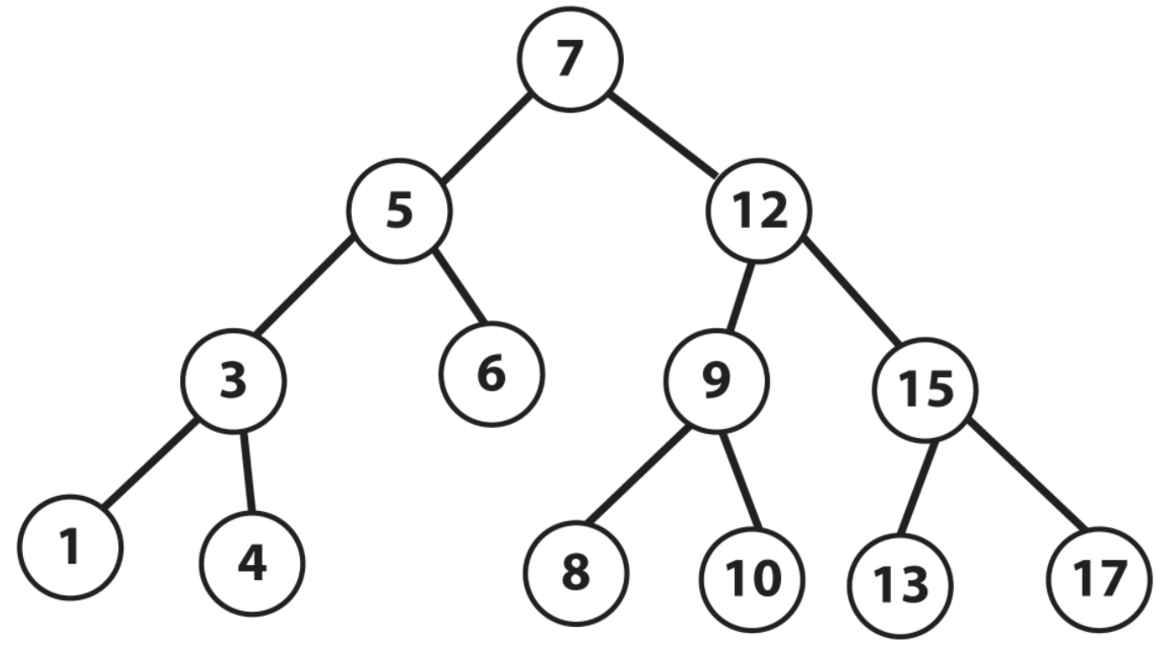
- AVL 트리, 레드 -블랙 트리 : 높이를 균형 있게 유지'

- 힙 (Heap):
- 우선순위 큐 구현.
- 최대 힙(Max Heap): 부모 ≥ 자식.
- 최소 힙(Min Heap): 부모 ≤ 자식.

- 트라이 (Trie) : 문자열 검색에 특화된 트리

시간 복잡도
| 연산 | 시간 복잡도 |
| 삽입 | O(log n) |
| 삭제 | O(log n) |
| 검색 | O(log n) |
활용 사례:
- 데이터베이스 인덱스.
- 파일 시스템.
- 조직도
- 토너먼트
- 가계도
그래프 (Graph)
정의
- 노드(장점) 과 간선(연결)으로 구성된 자료구조
구조
- 인접 행렬 (Adjacency Matrix):
- 2D 배열로 간선 표현.
- 인접 리스트 (Adjacency List):
- 연결 리스트로 간선 표현.
종류
- 방향 그래프 / 무방향 그래프:
- 간선에 방향이 있는지 여부.
- 간선에 방향이 있는지 여부.


- 가중치 그래프 (Weighted Graph):
- 간선에 가중치가 있는 그래프.

시간 복잡도
연산 인접 행렬 인접 리스트
| 간선 추가 | O(1) | O(1) |
| 간선 탐색 | O(1) | O(n) |
활용 사례
- 최단 경로 탐색 (다익스트라, A* 알고리즘).
- 네트워크 분석.
해시 테이블 (Hash Table)
정의
- 키(Key) 와 값 (Value) 쌍으로 데이터를 저장하며, 키를 해시 함수(Hash Function) 를 통해 버킷(Bucket)에 매핑
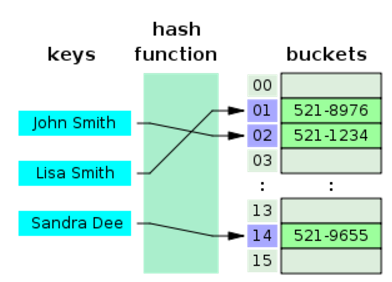
충돌 처리
체이닝 (Chaining) : 충돌 데이터를 연결 리스트로 저장

개방 주소법 (Open Addressing) : 선형 탐사, 이차 탐사, 이중 해성 등으로 충돌 해결

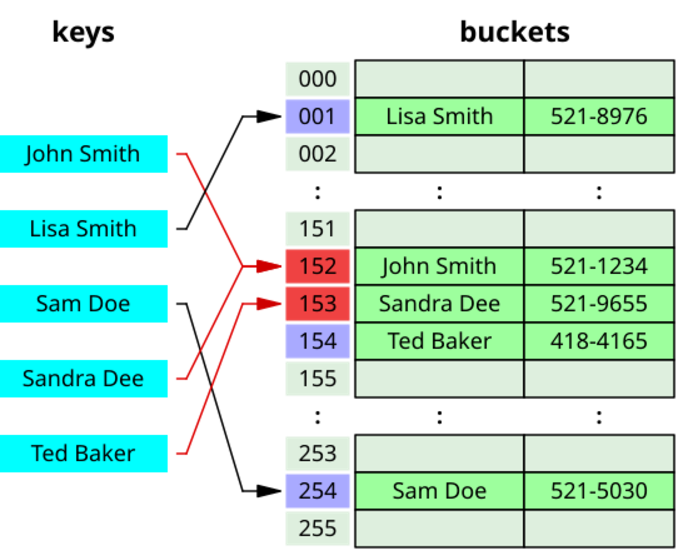
체이닝 (Chaining)의 장점
→ 연결 리스트만 사용하면 된다. 즉, 복잡한 계산식을 사용할 필요가 개방주소법에 비해 적다
→ 해시테이블 채워질수록, Lookup 성능저하가 Linar 하게 발생한다.
개방주소법 (open Addrssing)의 장점
→ 체이닝처럼 포인터가 필요업고, 지정한 메모리 외 추가적인 저장공간도 필요업삳
→ 삽입, 삭제시 오버헤드가 저가
→ 저장할 데이터가 적을 때 더 유리하다
시간 복잡도
| 연산 | 평균 시간 복잡도 | 최악 시간 복잡도 |
| 삽입 | O(1) | O(n) |
| 삭제 | O(1) | O(n) |
| 검색 | O(1) | O(n) |
활용 사례
1. 캐싱(Cache)
2. 데이터베이스 : 키 - 값 매핑
3. 문자열 거맥
요약
자료구조 특징 시간 복잡도 (검색/삽입/삭제) 활용 사례
| 배열 | 고정 크기, 인덱스 접근 가능 | O(1) / O(n) / O(n) | 행렬, 고정 크기 데이터 저장 |
| 연결 리스트 | 동적 크기, 삽입/삭제 효율적 | O(n) / O(1) / O(1) | 대기열, 메모리 재활용 |
| 스택 | LIFO 구조 | O(1) / O(1) / O(1) | 함수 호출 관리, 괄호 짝 검사 |
| 큐 | FIFO 구조 | O(1) / O(1) / O(1) | 작업 대기열, 네트워크 패킷 처리 |
| 트리 | 계층적 구조 | O(log n) / O(log n) / O(log n) | 데이터베이스, 파일 시스템 |
| 그래프 | 네트워크 구조, 노드와 간선 | O(1) / O(1) / O(n) | 최단 경로 탐색, 네트워크 분석 |
| 해시 테이블 | 키-값 매핑, 평균 O(1) 접근 속도 | O(1) / O(1) / O(1) | 캐싱, 문자열 검색 |